Chapter 9. Application of the Power Law and SRET Models to Bitcoin Market Cap
A 2019 change occurred in the growth rate of Bitcoin market cap. The popular "Twitter" Power Law model of Giovanni Santostais is wrong, an illusion of linearity created by a mistuned Power Law model.
9.1 Overview
In Chapter 8, growth of Bitcoin network size was modeled by the Power Law and Square Root of Elapsed Time (SRET) approaches. In Chapter 9, these two models are applied to the growth of Bitcoin market cap.
As noted in Chapter 8, the models will focus on the period between Bitcoin price bubbles — periods when growth of Bitcoin network value is related to the growth of network size and time.
A modeling strategy was developed in Chapters 6 and 7 based on examination of 14 historic technology adoptions of the 20th and 21st century. The SRET model was shown to be suitable for identifying technology adoption periods in both chapters, but the Power Law model with 0 time offset was not suitable for the 7 technology adoptions in Chapter 7.
This sequential strategy was applied in Chapter 8, and will be repeated in Chapter 9.
Model the market cap using the SRET model to identify adoption periods.
Model the market cap using the Power Law model, and examine for discontinuities indicating the need for a Power Law time offset.
If needed, apply the Power Law time offset to appropriated linearize the data and eliminate discontinuities between adoption periods.
9.2 Examination of a Semilog Plot of Bitcoin Market Cap
A semilog plot of Bitcoin market cap versus time was presented in Chapter 8 (Fig 8.1). The data between price bubbles exhibits the growth behavior typical of technology adoptions (i.e., rapid but decelerating growth, as discussed extensively in Chapters 6 and 7).
The history of Bitcoin market cap data begins on 17Jul2010, Day 1 of Bitcoin price history data in the Glassnode database. This convention for dating of Bitcoin market cap is maintained in these Substack chapters.
The modeling in this Substack typically begins on 01Jan2012, Day 534 of Bitcoin price history. There were three reasons for this decision. First, the price history in the earliest days is not believed to be well-connected to the growth of the Bitcoin network. For example, the price did not change in the first 100 days after 17Jul2010 — I.e.,, there was no evidence of price discovery during this period. This initial period of Bitcoin price history was then followed by Bitcoin’s first price bubble of 2011.
A second reason for modeling starting on 01Jan2012 is that Bitcoin-containing network addresses did settle down as a metric for network size until after that initial 533-day period following17Jul2010. One of the goals of the modeling effort in this Substack is development of a network value model (as described in Chapter 5), which requires a stable metric for the growth of network size.
The third reason for commencing modeling on 01Jan2012 is that little or nothing is lost by that decision. More than 90% of Bitcoin price history is captured after that date — i.e., plenty of history to understand the current trajectory of Bitcoin market cap and price.
9.3 Examination of Bitcoin Market Cap by the SRET Model
In 2018, there was a significant decrease in the growth rate of Bitcoin network size, as demonstrated by both SRET and Power Law models in Chapter 8. Metcalfe’s Law states that the growth of network value is related to the growth of network size. It is therefore entirely possible, even likely, that a decline in the growth rate of market capitalization occurred in the same time period.
The modeling of Bitcoin market cap was therefore divided into two modeling efforts: modeling the periods from 2012 through 2018 (Period 1) and 2019 to 01Jul2024 (Period 2). If there was no Bitcoin market cap regime change in 2018/2019, the models for the two periods should be aligned and show little or no change in slope. The specific cutoff date between Periods 1 and 2 was 01Jan2019, the approximate point determined iteratively when the Period 1 and 2 models intersect in the market cap analysis.
Important Note: The transition date between Period 1 and Period 2 was 01Sep2018 for modeling Bitcoin-containing containing address adoption in Chapter 8, and 01Jan2019 for modeling Bitcoin market cap in Chapter 9. It is not clear at this point in time whether this difference in transition date is real, or might just reflects noise in the Bitcoin market cap data in Period 2. The R2 for Period 2 was on the order of just 0.93 for both SRET and Power Law modeling of that period.
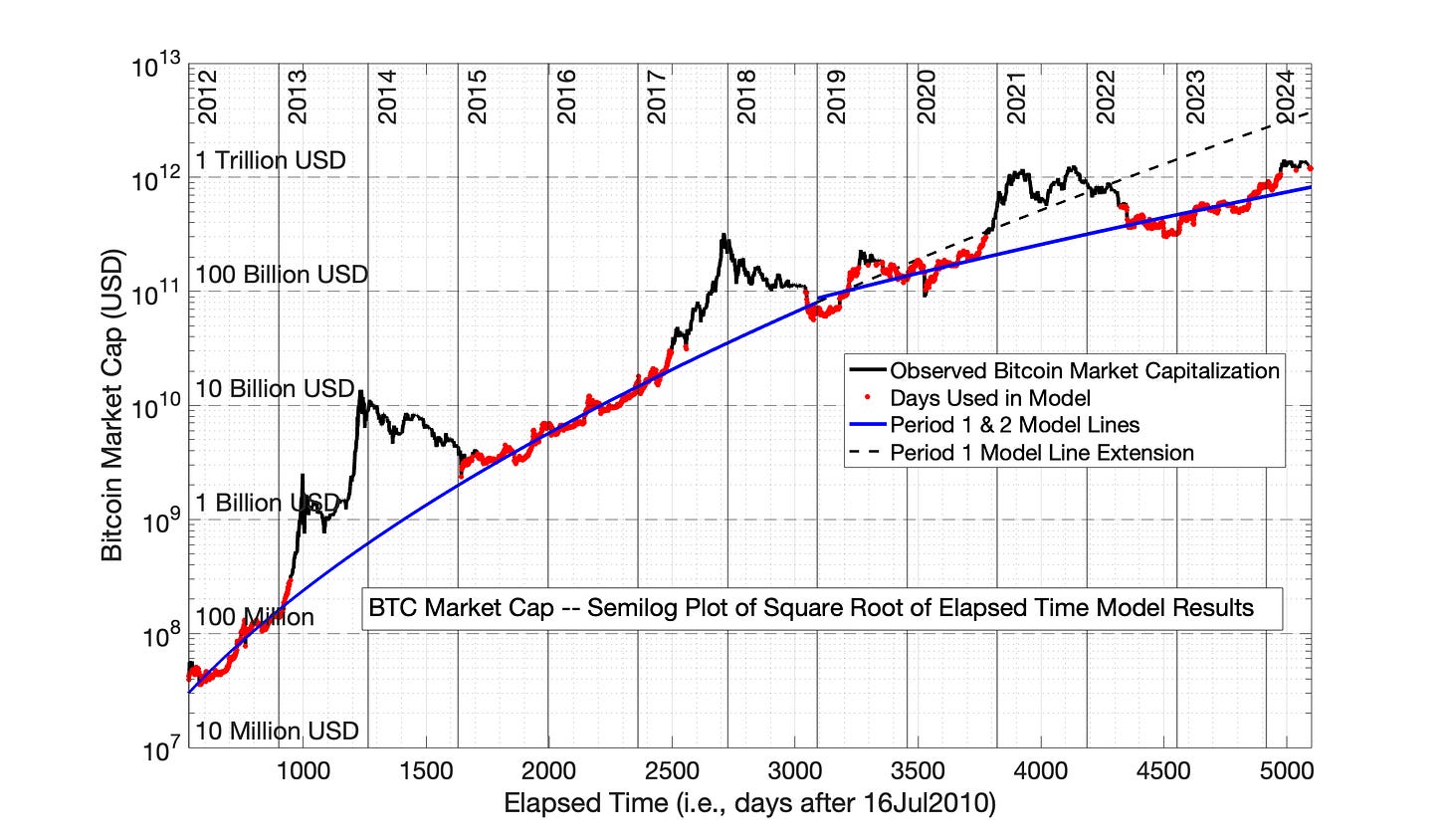
The Square Root of Elapsed Time (SRET) model for Bitcoin market cap is presented as Fig 9.1. The conventions established in Chapters 6, 7 and 8 are maintained:
Individual periods are shown as blue and red solid lines;
The black dashed line represents the Period 1 relationship extended into Period 2, providing a visual means to gauge the adoption rate change between Periods 1 and 2.
The vertical, dotted red line is the temporal midpoint of the graph, while the dotted blue line is the visual midpoint. The horizontal distance between these two lines is a measure of the time distortion created by the model. (As noted in Chapters 6 and 7, time distortion is the feature of the SRET and Power Law models that allows linearization of technology adoption data. See Section 7.2 and Figures 7.1, 7.2 and 7.4.)
The best-fitting, market cap model lines in Fig 9.1 are created by the same iterative procedure described in Chapter 8, Section 8.3 for determining the equations for BTC address models lines. The criterion for choosing the “red” days to be employed in the modeling the blue “fair value” lines of Fig 9.1 is that these days should have a market cap of not more than 3/2 of the fair value and not less than 2/3 of the fair value line — i.e., a range of about 0.6667 to 1.5 of the blue model line on that day. The upper limit of this range was chosen to capture about half of Bitcoin’s history, and exclude the days when Bitcoin was entering bubble territory (See Fig 9.1).
The lower end of this range was added to create a mathematically symmetrical range — i.e., the middle of the range is 2/3 of the upper limit, and lower limit is 2/3 of the middle. The middle of the range is 50% above the lower limit, and the upper limit is 50% above the middle. In fact, the only days following below the lower limit are a few days following the “Covid crash” of May, 2020 (See Fig 9.1).
A semilog plot of the market cap data and SRET model results is presented as Fig 9.2. Figures 9.1 and 9.2 demonstrate a change in Bitcoin market cap adoption trajectory starting in 2019. (It is not clear at this time whether the difference between the the onset of Period 2 in Chapters 8 and 9 Is real, or just an artifact of Bitcoin data variability.)
The SRET model formulas for the Period 1 and 2 “blue” lines of Fig 9.1 are:
Period 1: ln(market cap) = 0.2428*sqrt(elapsed time) +11.61
Period 2: ln(market cap) = 0.1420*sqrt(elapsed time) +17.29
Where ln, sqrt, and * are the symbols for natural logarithm, square root and multiplication, respectively. Market cap is in US dollars and elapsed time is in days after 16Jul2009 — that is, Day 1 is 17Jul2010.
In Table 9.1, the SRET model results of Figures 9.1 and 9.2 are translated into a table of Bitcoin market cap and price values from 2012 to 2024, with some modest extrapolation of the Period 2 relationship into the future.
Note: The extrapolation of the Period 2 relationship into the future is for educational purposes only, and should not be interpreted as investment advice. The history of technology adoptions presented in Chapters 6 and 7 demonstrate that regime changes occur regularly in the history of technology adoptions. It is hypothetically possible that a new regime change is already underway for Bitcoin market cap, and the future projections of Table 1 are irrelevant.
Fig 9.1 Bitcoin Market Capitalization: SRET model. Bitcoin market cap is evaluated by the SRET model independently in 2 periods: Period 1: from 01Jan2012 to 01Jan2019 and Period 2: from 01Jan2019 to 01Jul2024. The least-squares, best-fitting straight lines are shown in solid blue for the two periods (Fig 9.1). Days employed to generate these best-fitting straight lines are in red. The black dashed line is the extension of the Period 1 model line into Period 2, to provide a visual reference for the change of adoption rate in Period 2. The R2 for Periods 1 and 2 were 0.995 and 0.933, respectively.
Fig 9.2 Bitcoin Market Capitalization: SRET model results from Fig 9.1 plotted semilog versus time. The data and SRET model equations demonstrate the rapid but decaying growth rate typical of technology adoptions. The meanings of the solid blue and red lines and the dashed black line are same as in Fig 9.1.
Table 9.1 Bitcoin market cap history from the Square Root of Time (SRET) model for Periods 1 and 2. The blue and red, best-fitting lines of Fig 9.1 are translated into annual percentage increases for market cap and price. Numbers in red represent projections of the Period 2 model into the future. Please note: See the note in the text about the uncertainty associated with projecting future Bitcoin market cap and price.
9.4 Examination of Bitcoin Market Cap by the Power Law Model
The Power Law model is applied to Bitcoin market cap data in Figures 9.3, 9.5, 9.7 and 9.9 for time offsets of 0, 560, 1000 and 2000 days. Fig 9.3 is the Power Law model wot 0 day offset. A Power Law time offset of 560 days (1.5 years) is the value employed in the version of the Power Law frequently presented on Twitter (X.com). (Reference: Giovanni Santostasi, “The Bitcoin Power Law Theory”, Medium.com, 20May2024).
The 2000 day (5.5 year) time offset was the value determined in Chapter 8 to eliminate model discontinuity between Periods 1 and 2 for the Power Law modeling of Bitcoin network size adoption. The time offset of 1000 days was added to better illustrate model behavior between time offsets of 560 and 2000 days.
The blue, Power Law model lines in Figures 9.3 (0 day offset), 9.5 (560 day offset), 9.7 (1000 day offset) and 9.9 (2000 day offset) were each determined by the same iterative procedure employed for determining the blue SRET model lines in Fig 9.1.
The Power Law with 0 day time offset in Fig 9.3 and Fig 9.4 demonstrates a clear discontinuity between Periods 1 and 2. Based on data presented in Chapters 7 and 8, this demonstrates that the Power Law with 0 day time offset is over-adjusting data points too far to the right in Period 1 (e.g., Fig 7.1) — that the Power Law with 0 day time offset is too powerful to appropriately model the growth of Bitcoin market cap. Therefore, the modeling of Bitcoin market cap with the Power Law model falls into the category of the adoptions presented in Chapter 7.
The discontinuity between Periods 1 and 2 in Figures 9.3 and 9.4 is directly analogous to the same discontinuity seen in Figures 8.5 and 8.6 for the modeling the growth profile of Bitcoin-containing addresses.
Fig 9.3 Bitcoin Market Capitalization: Power Law model with 0 day time offset Bitcoin market cap is evaluated by the SRET model independently in 2 periods: Period 1: from 01Jan2012 to 01Jan2019 and Period 2: from 01Jan2019 to 01Jul2024. The discontinuity between the Period 1 and Period 2 results reflects over-adjustment to the right of early data points by the Power Law with 0 time offset. The R2 for Periods 1 and 2 were 0.993 and 0.934, respectively.
Fig 9.4 Bitcoin Market Capitalization: Power Law model with 0 day time offset results from Fig 9.3 plotted semilog versus time. The discontinuity between Periods 1 and 2 from Fig 9.3 is clearly reflected in this semilog plot.
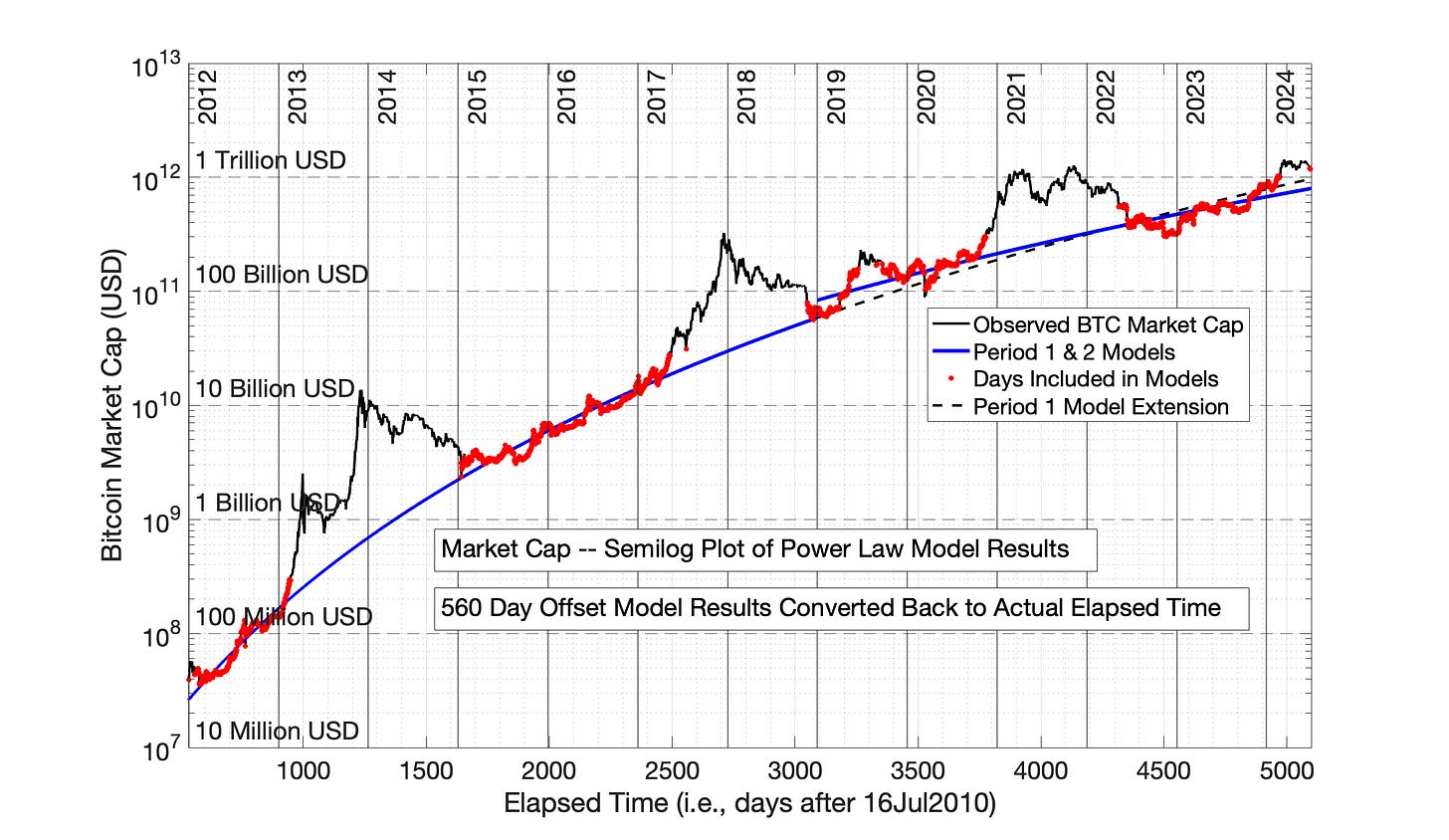
Figures 9.5 and 9.6 demonstrate the impact of a 560 day offset for the Power Law model. The reduction in Power Law time over-adjustment by the 560 day offset has reduced, but not eliminated, the discontinuity between at the period intersection. However, this intermediate value of Power Law model time offset creates a false impression of a consistent Bitcoin market cap growth trajectory across Bitcoin history.
That is, an observer looking at the data of Fig 9.5 (i.e., independent of the two, Period 1 and 2 blue lines) could be deceived into believing that the red data values represent a single period from 01Jan2012 to 01Jul2024. Similar misleading scenarios were observed in Chapter 7 for other historic technology adoptions (Figures 7.12 and 7.25).
Fig 9.5 Bitcoin Market Capitalization: Power Law model (560 day offset) This intermediate value of Power Law time offset has created a false impression of a consistent market cap growth trajectory across Bitcoin market cap history. The R2 for Periods 1 and 2 were 0.995 and 0.933, respectively.
Fig 9.6 Bitcoin Market Capitalization: Power Law model equations (560 day offset) from Fig 9.5 plotted semilog versus time. This intermediate value of Power Law offset has created a false impression of a single period of market cap growth across Bitcoin history.
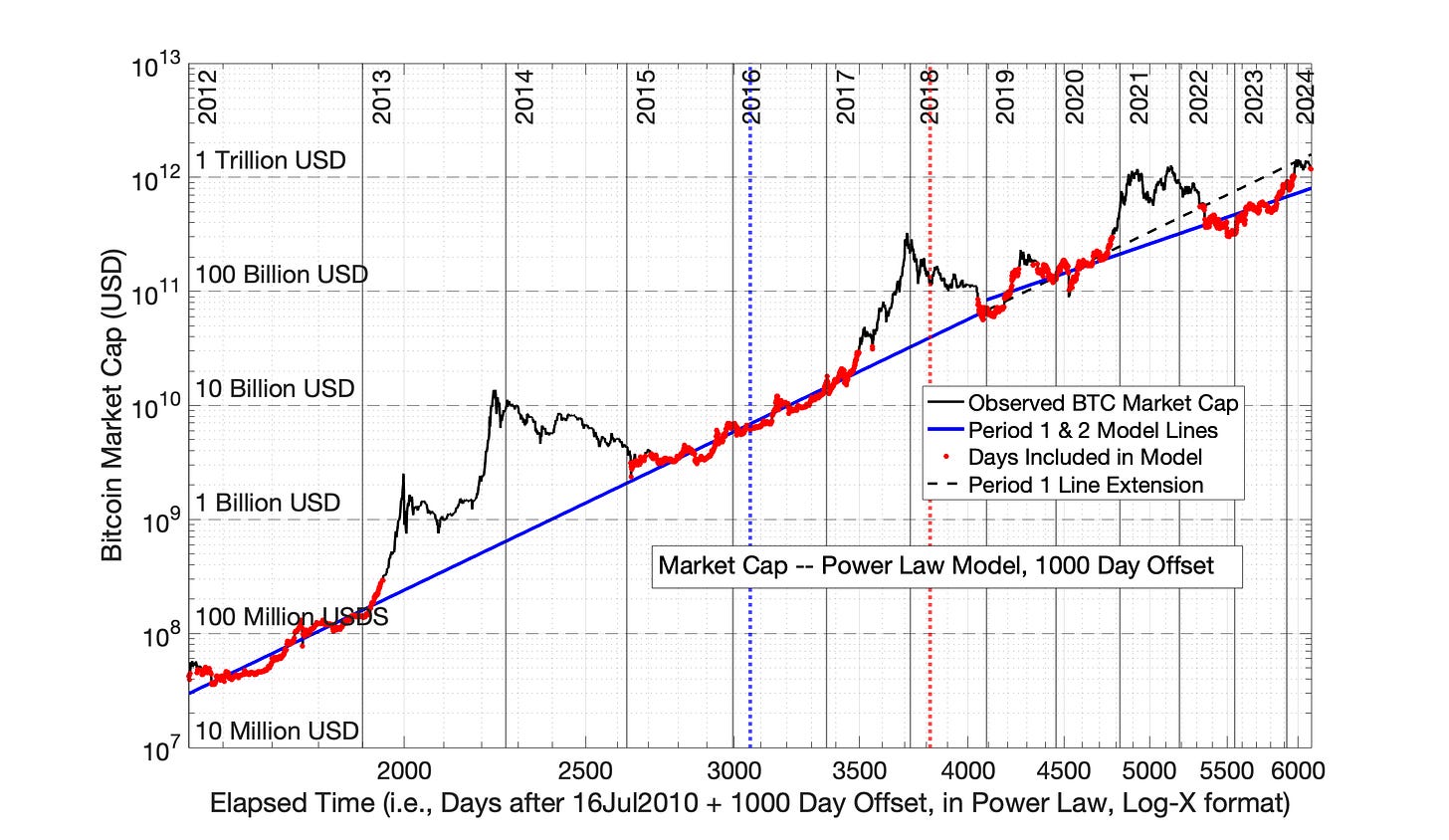
Figures 9.7 and 9.8 demonstrate the impact of a 1000 day time offset (~2.7 years). The purpose of adding these two figures is to more clearly show the transition of Power Law model results from the 560 day offset to the 2000 day offset. That is, in Fig 9.7, the discontinuity between the blue lines at the period intersection has been reduced relative to Fig 9.5, but not eliminated.
Fig 9.7 Bitcoin Market Capitalization,: Power Law model equations (1000 day time offset) The Power Law with 1000 day time offset (~2.7 years) reduces the discontinuity seen between Periods 1 and 2 — that is, relative to Fig 9.5. The R2 for Periods 1 and 2 were 0.995 and 0.935, respectively
Fig 9.8 Bitcoin Market Capitalization: Power Law model equations from Fig 9.7 plotted semilog versus time. The Power Law with 1000 day time offset (~2.7 years) reduces the discontinuity seen between Periods 1 and 2 — that is, relative to Fig 9.6.
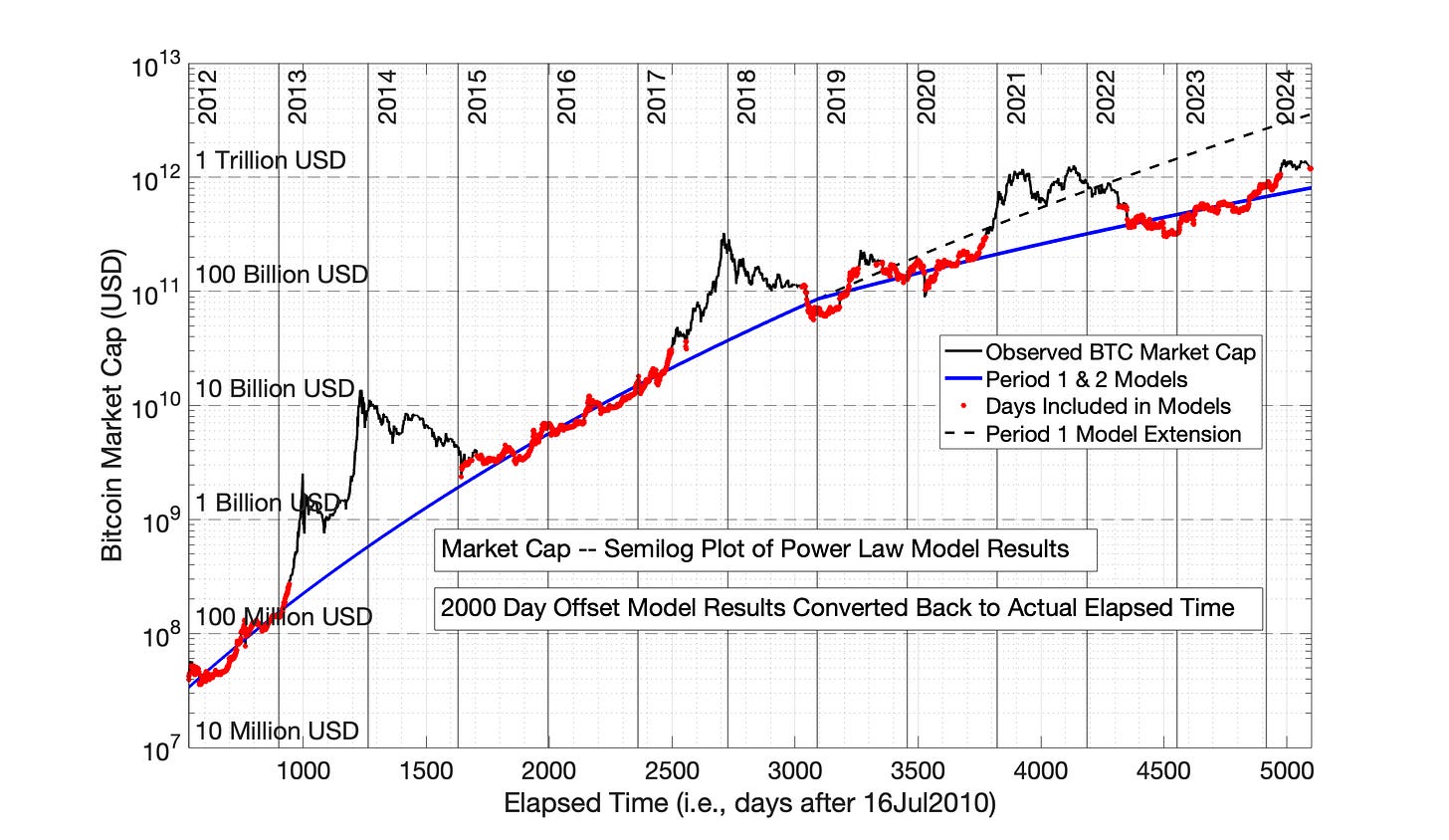
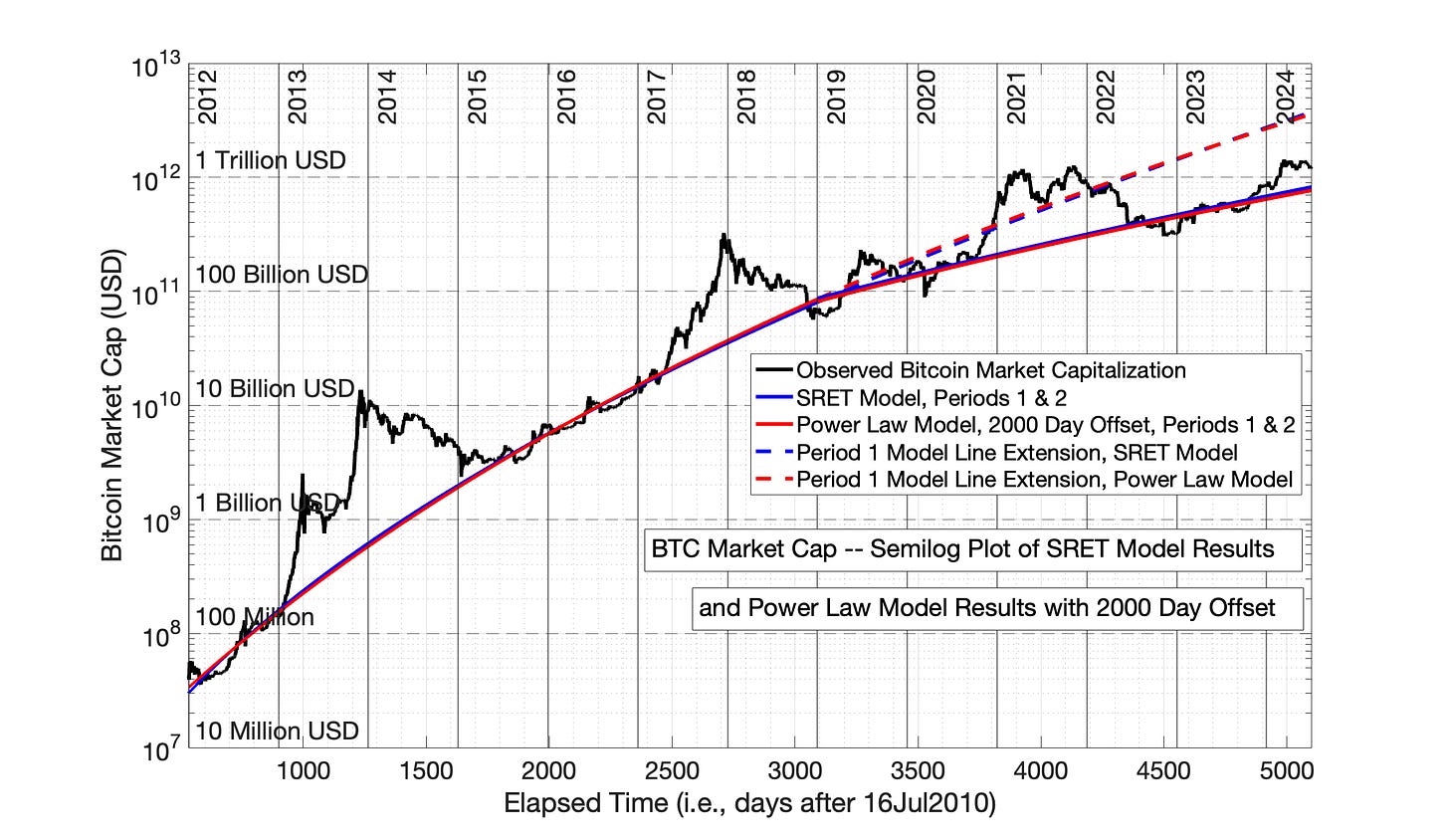
Figures 9.9 and 9.10 demonstrate the impact of a 2000 day offset (5.5 years) for the Power Law model of Bitcoin market cap. The 2000 day offset eliminates the offset between Periods 1 and 2, indicating that this is the correct Power Law time offset — a result similar to Chapter 8 for network size. This offset also brings the Power Law into approximate alignment with the SRET model (Figures 9.1 and 9.2), another result shared with the Power Law model with 2000 day offset of Bitcoin network size in Chapter 8 (Compare Figures 8.9 and 8.10 with Figures 8.3 and 8.4).
Fig 9.11 presents results from the SRET model and Power Law model (with 2000 day offset) together on the same semilog plot as a function to time. The SRET model results are the solid blue, Period 1 and 2 lines. The Power Law model (with 2000 day offset) are the solid red, Period 1 and 2 lines. The dashed blue and red lines are the extensions of the Period 1 models into Period 2, to better illustrate the decline in market cap adoption rate growth observed in Period 2. The results of the SRET model and Power Law model (with 2000 day offset) applied to Bitcoin market cap are within 10% of each other throughout the period of Fig 9.11 (data not shown).
The alignment of the SRET model results and Power Law model (2000 day time offset) is consistent with all of the results presented previously in Chapters 7 and 8. Modeling Bitcoin market cap falls into the same category as the 7 technology adoptions of Chapter 7 and the modeling of Bitcoin network size in Chapter 8.
Fig 9.9 Bitcoin Market Capitalization,: Power Law model equations (2000 day time offset) The Power Law with 2000 day time offset (5.5 years) eliminates the discontinuity between Periods 1 and 2, and produces results comparable to the SRET model (Fig 9.1). The R2 for Periods 1 and 2 were 0.995 and 0.934, respectively
Fig 9.10 Bitcoin Market Capitalization: Power Law model equations from Fig 9.9 plotted semilog versus time. The Power Law with 2000 day time offset (5.5 years) eliminates the discontinuity seen between Periods 1 and 2, and produces results comparable to the SRET model (Fig 9.2).
Fig 9.11 Bitcoin Market Capitalization: SRET and Power Law model equations presented together semilog versus time. The Power Law with 2000 day time offset (5.5 years) eliminates the discontinuity seen between Periods 1 and 2, and produces results within plus-or-minus 10% the SRET model (Fig 9.2).
The following model equations are presented for completeness, and to reinforce the meaning of the time offset in the Power Law model.
The blue, best-fitting straight lines in Fig 9.3 (Power Law, 0 Day Offset) have the model formulas
Period 1: ln(market cap) = 4.390*ln(elapsed time) - 10.83
Period 2: ln(market cap) = 4.512*ln(elapsed time) - 11.12
The blue, best-fitting straight lines in Fig 9.5 (Power Law, 560 Day Offset) have the model formulas
Period 1: ln(market cap) = 6.403*ln(elapsed time + 560) - 27.73
Period 2: ln(market cap) = 5.148*ln(elapsed time + 560) - 17.08
The blue, best-fitting straight lines in Fig 9.7 (Power Law, 1000 Day Offset) have the model formulas
Period 1: ln(market cap) = 7.890*ln(elapsed time +1000) - 40.67
Period 2: ln(market cap) = 5.646*ln(elapsed time +1000) - 21.80
The blue, best-fitting straight lines in Fig 9.9 (Power Law, 2000 Day Offset) have the model formulas
Period 1: ln(market cap) = 11.24*ln(elapsed time +2000) - 70.76
Period 2: ln(market cap) = 6.747*ln(elapsed time +2000) - 32.41
9.5 Summary of Data and Analysis in Chapters 6, 7, 8, and 9
In this section, the analyses presented in these 4 chapters will be systematically presented. The first 20 observations/results presented below lead to the conclusion of observation 21 that the popular Power Law model of Giovanni Santostasi presented frequently on Twitter is wrong.
that this popular “Twitter” model is based on an improper choice of Power Law time offset.
that the presumption of this Twitter model that Bitcoin market cap has experienced a single period of linear growth is wrong. Bitcoin experienced a downshift in adoption rate for both network size and market cap in the 2018/2019 period.
To justify such strong statements, it is important to systematically present the observations/results leading to those conclusions. In that spirit, 20 sequential observations/results from Chapters 6, 7, 8, and 9 are presented below.
1. Fourteen historic technology adoptions have been analyzed in these Substack Chapters 6 and 7. All of these technology adoptions share a common form when plotted semilog as a function of time. They exhibit continuous, rapid growth, but with a decelerating annual growth rate.
2. The gold standard for any mathematical model of technology adoption is to find a mathematical formula that allows one to plot adoption data as a straight line — “a mathematical model that linearizes the data.” With such a mathematical formulation, technology adoption can be expressed as y = m*x + b, where m and b are the slope and intercept, respectively.
The Power Law model has the form
ln(N) = n*ln(elapsed time + time offset) + d
Where “ln” is the symbol for natural log, * is the multiplication symbol, and N is the symbol for network size (or network value). Time offset is a specific constant greater-than-or-equal to zero.
The constants n and d are the slope and y-intercept, respectively.
This model is an excellent fit for any technology adoption data that plots as a straight line when plotted as ln(N) versus ln(elapsed time + time offset).
The formula for the Square Root of Elapsed Time (SRET) model is network size (or network value) is
ln(N) = m*sqrt(elapsed time) + b,
Where “sqrt” is symbol for square root
The constants m and b are the slope and y-intercept, respectively.
This model is an excellent fit for any technology adoption data that plots as a straight line when plotted as ln(N) versus sqrt(elapsed time).
3. In spite of their different equation formats, the Power Law model and the SRET model are both capable of linearizing technology adoption data. This is demonstrated through analysis of 14 historic technology adoptions in Chapters 6 and 7.
4. A good way to understand how the Power Law and SRET models are achieving data linearization is to follow the movement of individual data points from a curved semilog adoption plot to a linearized format in a plot of the SRET model or Power Law model. This was the purpose of Section 7.2, Figures 7.1, 7.2 and 7.4. The Power Law model and the SRET model achieve their success by differentially moving the position of individual technology adoption points in time.
Conceptually, consider the original adoption data (plotted semilog vs time, as in Fig 7.1) is divided into 4 quadrants — i.e., earliest 25% of data, next 25% of data, etc. Both the Power Law model and the SRET model move the data in the 2nd quadrant the most, followed by the 1st and 3rd quadrant, followed last by the 4th quadrant (Section 7.2.)
5. The Power Law model with 0 time offset and the SRET model are not identical in their ability to linearize adoption data. In the example presented in Section 7.2, the standard Power Law model with 0 time offset moves individual data points almost twice the distance of the SRET model, as indicated by the blue and red arrows in Fig 7.1. This is also obvious in the comparison of Power Law model and SRET model plots for each of the 7 historic technology adoptions presented in Chapter 6 — e.g., compare Figures 6.2, 6.3 and 6.5. The Power Law model with 0 time offset is “more powerful” or “more intense” in its adjustment of technology adoption data points.
6. In spite of this difference in data-movement intensity, both the Power Law with 0 time offset and SRET models effectively linearize adoption data and identify the same technology adoption periods in the 7 historic technology adoptions of Chapter 6. The Power Law model with 0 time offset was clearly better than the SRET model for linearizing some adoption periods for the technology adoptions in Chapter 6 — for example, compare the 2nd, “red” period in Fig 6.3/6.4 (Power Law plots) with the same period in Fig 6.5/6.6 (SRET model plots). This superiority of the power law model with 0 time offset in linearizing an individual adoption period with strong curvature was repeated in 5 of the 7 technology adoptions of Chapter 6, as identified in Section 6.6.
7. For the 7 historic technology adoptions in Chapter 7, the SRET model was very effective in linearizing technology adoption data and identifying the proper adoption periods. That is, the SRET model was effective in identifying technology adoption periods in all 14 technology adoptions in Chapters 6 and 7.
8. The over-adjustment of data by the standard Power Law with 0 time offset is manifest for each of the 7 historic technology adoptions presented in Chapter 7. For example:
single adoption periods when plotted by the SRET model become two periods in a convex orientation when plotted by the Power Law model (compare Figures 7.2 and 7.4, 7.30 and 7.32, and 7.60 and 7.62).
data points are rearranged into new adoption periods by the Power Law model when compared to the SRET model (compare Figures 7.7 and 7.9; 7.20 and 7.22; 7.40 and 7.42; 7.50 and 7.52) and
discontinuity between adoption periods in the Power Law model (e.g., see Figures 7.22/7.23 and Fig 7.9/7.10).
9. The over-adjustment of data by the Power Law model in the Chapter 7 examples can be corrected in each case by the addition of a time offset to the adoption data. This changes the Power Law formula from ln(N) = n*ln(elapsed time) + d to
ln(N) = n*ln(elapsed time + f) + d, where f is a positive time offset
A simple example of application of a time offset is presented in Section 7.3.
The Power Law time offset was effective in linearizing the adoption data and identifying correct adoption periods for each of the 7 technology adoptions in Chapter 7 — for example, compare Figures 7.4 and 7.6, 7.9 and 7.11, 7.22 and 7.24, 7.32 and 7.34, 7.42 and 7.44, 7.52 and 7.54, and 7.62 and 7.64.
10. Thirteen of the 14 examples of Chapter 6 and 7 were chosen from a relatively small set of about 25 technology adoptions described on the website ourworldindata.org (described in Sections 6.7 and 7.9, respectively). The 14 chosen historic adoptions segregate into two equal groups in Chapters 6 and 7. This doesn’t mean that the two categories represented by Chapters 6 and 7 will be equal in size when examining a broader group of technology adoptions. But, it is does indicate that these are likely to represent two substantial subgroups of technology adoptions.
11. A conclusion based on the evaluation of the 14 technology adoptions presented in Chapters 6 and 7 is that the SRET model is best able to identify the correct technology adoption periods. Conversely, the Power Law model is not well-suited to properly identify adoption periods (Chapter 7). One example was US adoption of home refrigeration, where the Power Law exhibited three distinct adoption profiles depending upon the choice of time offset — 0, 1 and 5 years. (Figures 7.9, 7.11, and 7.12)
12. None of the 14 historic technology adoptions from Chapter 6 or 7 proceeded as a single linear period from start to finish, when modeled by either the Power Law model or the SRET model. Multiple adoption periods appear to be the expectation in technology adoption. A technology adoption that proceeds as a single adoption period from 1% adoption to nearly 100% adoption appears to be either infrequent or non-existent. Most technology adoptions have multiple adoption periods when appropriately modeled by the SRET and Power Law approaches.
13. The Power Law model with time offset was introduced in Chapter 7. The time offset is not often mentioned explicitly in conjunction with the Power Law model, but its use is implicit in the establishment of Day 1 for the adoption data. For example, the true Day 1 of Bitcoin price and market cap history is 17Jul2010 in the Glassnode database. But, the most popular “Twitter” application of the Power Law for Bitcoin recasts Day 1 as Jan 3, 2009. The actual Day 1 (17Jul2010) becomes Day 561 in this new Twitter Bitcoin model formulation.
In this Substack, Bitcoin Day 1 is maintained as 17Jul2010, and the popular Bitcoin “Twitter” Power Law model noted above has a time offset of 560 days — the is, the model equation for the popular Twitter Bitcoin model is:
ln(N) = n*ln(elapsed time + 560) + d.
14. An analysis of Bitcoin network size adoption in Chapter 8 provides clear evidence that Bitcoin network size adoption rate experienced an adoption regime change in 2018. For the self-custody user count data presented in the Appendix, the 2018 regime change was evident in the semilog plot versus time (Fig 8.12), and was further clarified by SRET model (Fig 8.13) and the Power Law model, with 0 offset (Fig 8.15), 560 day time offset (Fig 8.17) and 2000 day time offset (Fig 8.19). This 2018 regime change is probably obvious to many people in the semilog lot versus time of Bitcoin-containing address data (Fig 8.1), but this 2018 shift is absolutely clear in the SRET model analysis (Fig 8.3) and the Power Law analysis with 2000 day time offset (5.5 years, Fig 8.9).
15. In contrast, the analysis of Bitcoin-containing address count by the Power Law with time offsets of 0 days and 560 days produced plots consistent with Power Law data over-adjustment, like the 7 historic technology adoptions of Chapter 7. The Power Law model (time offset of 0) resulted in a significant discontinuity between Periods 1 and 2 (Figures 8.5 and 8.6). This result is consist with heightened data adjustment in the 2nd quadrant of the original semilog plot of adoption data of Fig 8.1, resulting in a Period 1 plot in Fig 8.5 that is over-adjusted to the right, creating the discontinuity. The time offset of 560 days reduced the data discontinuity between Periods 1 and 2, but did not eliminate it.
16. Analysis of Bitcoin market cap by the Power Law with time offsets of 0 days and 560 days also produced plots consistent with Power Law data over-adjustment, like the 7 historic technology adoptions of Chapter 7. In fact, these plots (Figures 9.3, 9.4, 9.5 and 9.6) were very similar to the analogous plots for Bitcoin-containing addresses in Chapter 8 (Figures 8.5, 8.6, 8.7 and 8.8).
17. Analysis of Bitcoin market cap by the Power Law model with 2000 day time offset was very similar to the SRET model for Bitcoin market cap (Compare Figures 9.1 and 9.2 with Figures 9.9 and 9.10.) These results are very similar to the analogous plot for Bitcoin-containing addresses in Chapter 8 (Figures 8.3, 8.4, 8.9, and 8.10).
18. A side-by-side comparison of SRET model and Power Law model (with 2000 day time offset) for Bitcoin market cap analysis is presented as Fig 9.11. The two models remain within plus-or-minus 10% throughout the study period from Day 535 (01Jan2012) to Day 5099 (01Jul2024).
19. The market cap analysis by the Power Law with a suboptimal time offset of 560 days (Figures 9.5 and 9.6) was analogous to the disturbing results observed in the adoption of US home refrigeration, where a suboptimal choice of a one-year time offset produced results that infer a single adoption period (Fig 7.12). The optimal time offset for this technology adoption was 5 years (Fig 7.11).
20. As noted above, application of the Power Law with a time offset of 560 days is equivalent to the common Power Law application frequently presented on Twitter. This model apparently originated by Giovanni Santostasi. This model is presented in Fig 9.12, applying the same methodology employed to create the other SRET model and Power Law model plots in Chapter 9. A detailed description of the generation of Fig 9.12 is presented in the text following the figure.
21. In light of the 20 observations presented above:
The linearity of Fig 9.12, the popular Twitter Power Law model of Bitcoin market cap, is an artifact of Power Law over-adjustment of data points combined with a suboptimal choice of Power Law time offset.
The adoption of Bitcoin, as measured by market cap has not proceeded as a single, linear adoption period from 2010 to present, as suggested by Fig 9.5 and Fig 9.12.
Rather, there was shift in the growth rates of both market cap and market size in the 2018/2019 time period, as correctly shown by the SRET model and the Power Law model with 2000 day (5.5 year) time offset (Figures 9.1, 9.2, 9.9, 9.10, and 9.11)
Fig 9.12 The Incorrect, Popular Twitter Power Law Model of Bitcoin Market Cap. The Power Law model (with 560 days offset) is applied under the incorrect assumption of a single, linear adoption period from Day 1 (17Jul2010) to Day 5099 (01Jul2024). The least-squares, best-fitting straight line representing the model is in blue. Days employed to generate these best-fitting straight lines are in red. The procedure for determining the red data points is described in the text below. The R2 for the blue model line is 0.997.
Details of Fig 9.12 generation: This is a Power Law model with 560 day time offset for the Bitcoin market cap data from Day 1 (17Jul2010) to Day 5099 (01Jul2024). The “red” data points chosen to produce the single “blue” line in Fig 9.12 followed the procedure applied to produce all of the SRET and Power Law analyses in this chapter — that is the red data points are all less than 3/2 of the blue line value on the same day, and greater than 2/3 of the blue line value on that day. The least-squares, best-fitting, blue straight line was determined by the same iterative procedure employed in Chapters 8 and 9.
The blue, best-fitting straight line in Fig 9.12 has the model formula
ln(N) = 6.462*ln(elapsed time + 560) - 28.15
where elapsed time is in days after 16Jul2010 — that is, Day 1 is 17Jul2010.
9.6 Data Sources and Analysis
Bitcoin network data in this chapter are provided by the cryptocurrency analysis provider Glassnode (www.glassnode.com), as part of an “Advanced” membership plan at about $30/month.
Day 1 of Bitcoin price and market cap history in the Glassnode database is 17Jul2010. The Glassnode daily market cap and Bitcoin-containing address counts are numbered from Day 1 through Day 5099 (July 1, 2024). The period of primary focus is Day 534 (01Jan2012) to Day 5099.
Data analyses and preparation of figures were performed using Matlab (www.mathworks.com).
9.7 About the Author
The author has a B.S. and PhD. In chemical engineering. His PhD thesis focussed on mathematical modeling, simulation, and implementation of process control. Following his PhD, he was a university professor for 10 years at two US universities, focusing on both research and teaching. At both universities he taught the required chemical engineering course in process modeling and control. He subsequently spent more than 20 years in industrial chemical engineering practice.